中には「定員確定」「浜田ロジック」などと言った名称つきのテクニックを紹介しているものもある（これらを紹介している＝それがないと解けない難解作を扱っているナンプレ誌、という図式が成り立つ）。
当初はそっちの話を書こうとしたのだが、上記単語で検索するとこれらの内容（詳細）に触れている個人サイト（ブログなど含む）が沢山出てくるので、あえてこのブログでは扱わない事にした（せめて浜田ロジックの「浜田」の正体がわかれば話のネタにはなったのだが…）。
上記テクニックについて知りたい方がいたら、お手数だが上記単語で検索していただきたいと思う。
…が、その前に注意事項を１つ。ここから先は解き方を分かりやすく（？）説明する為に
画像（問題図）の一部が明滅するものが出てきます。
昔話題になった「ポケモンショック」ほどの明滅ではありませんが（喩えが古いって？ …すみません
）、見ていて体調を崩される方が出てこないという保証はないので、閲覧される時は十分な注意をしていただきたいと思います。
）、見ていて体調を崩される方が出てこないという保証はないので、閲覧される時は十分な注意をしていただきたいと思います。他のナンプレ、例えばスタンダードナンプレは１～９の数字を用いているが、よく考えるとこのパズルで用いるフィギュアが１～９の数字である必然性はどこにもない。仮に１～９を「あいうえお…」や「ＡＢＣＤＥ…」なんかに置き換えたところで何の不都合もないのである（※１）。
しかし不等号ナンプレは不等号によって数字の大小を指定する、つまり要所要所で「算数」が出てくるナンプレであり、人によっては見ているだけで頭が痛くなる可能性もあるかも知れないが、慣れてくるとスタンダードナンプレにはない面白さが見えてくる、場合によってはスタンダードナンプレを解くのがつまらなくなる可能性もある実に魅惑的な（？）ナンプレである。
なので、今回の記事を読んで不等号ナンプレを好きになる人が増えたら一人のパズル作家としての冥利に尽きる、というものである。
今回の例題には前々回に不等号ナンプレ（ブロックなし）を紹介する時に使ったものを使う事にする
（わざわざ別の問題を用意するのが面倒なだけ…
）。
）。
中には「こんなナンプレ解けるか」とか、今のご時世だと「作者死ね」などという暴言を吐く人もいそうである。
…そういう人はひとまず無視して、まずはこのナンプレを解く為の「取っ掛かり」を探す事にする。
なお、次の図から明滅箇所が出てきます。
①最小数字が入る箇所を探す
最小数字というのは読んで字の如く「最も小さい数字」である。
なので最小数字をＡとして不等号で示すと「Ａ＜○」（読み方は「Ａ小なり○」）となる。これを逆に考えると「Ａ＞○」は理論的にありえないことになる。
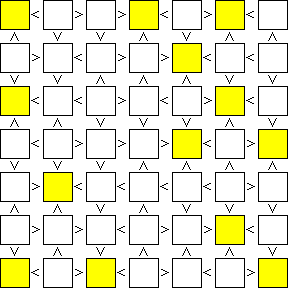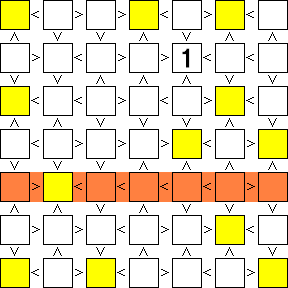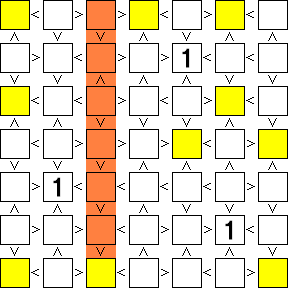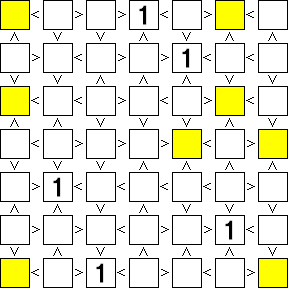
そこで、隣接する不等号が全て「小なり」であるマスを全てピックアップするのが不等号ナンプレを解くための第一歩である。
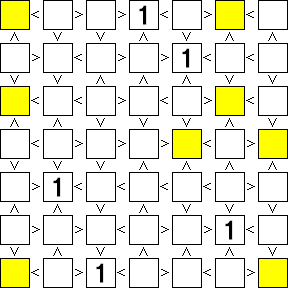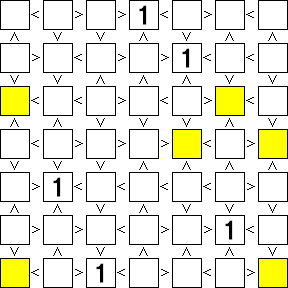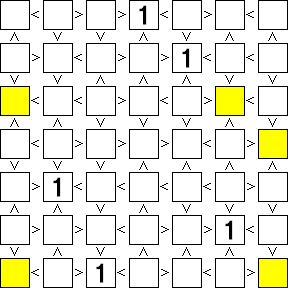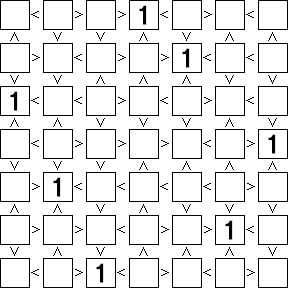
この例題の場合、下図の黄色で塗られた１３のマスがそれに該当する。
★実際に紙とペンで解く場合、いちいちマスを塗りつぶすのは面倒極まりないので、マスの肩に小さく「○」なり「×」なりを書くのがいいでしょう。
ナンプレの場合特に断りがない限り最小数字は「１」なので、黄色で塗られたマスには「１」が入る可能性がある、というより黄色で塗られなかったマスに「１」が入る事は絶対無い。
「１」が入る可能性のあるマスを絞り込んだら、次は実際に「１」を入れる作業に入る。
ナンプレの基本的なルールとして「全ての段（列）に１～○の数字が１つずつ入る」ので、１つの段（列）に黄色のマスが１つしかない場合は、そのマスが自動的に「１」に確定する。
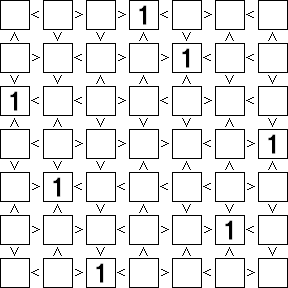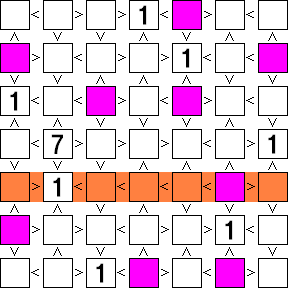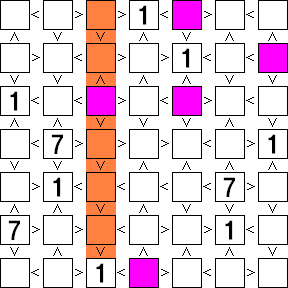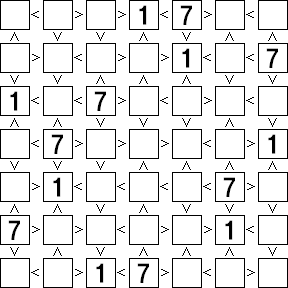
それを踏まえて「１」が確定するマスを探す。…すると下図のように５つの「１」が確定できる。
…いよいよ画面の明滅が激しくなってきました（笑）。「動画」を使えば明滅を止める事もできるのだが、（自分の）技術的にもブログの容量的にも断念してしまった…
「全ての段（列）に１～○の数字が１つずつ入る」ため、「１」が確定したマスと同じ段（列）にある黄色のマスに「１」が入る可能性は消滅する。そこで「１」が入る可能性のなくなった黄色のマスにはもう用がないので消えてもらう事にする。
すると黄色のマスが２つ残るので、その２マスにも「１」が確定する。
★時間短縮を考えると「１」が確定した瞬間に不要な黄色のマスを消すと少しは効率がいいのだが、慣れないうちにそれをやると間違え（見落とし）やすいので、最初のうちは「確定したマスに１を入れる」→「可能性の消えたマスを消す」→「残ったマスの中から確定するマスに１を入れる」→…とするのがいいと思います。
今回の例題では全ての「１」が確定したが、不等号の向きの関係でこの作業だけでは全ての「１」が確定できない場合もある。そういう場合は確定できるところだけ確定させて（残りはまた後にして）次の作業に移る事にする。
②最大数字が入る箇所を探す
次は最大数字を埋めていく。今回の例題はサイズが７×７なので、最大数字は「７」である。
具体的なやり方は最小数字を埋めるときと同様で、
・隣接する不等号が全て「大なり」であるマスをピックアップする（今回は紫色のマス）
・同じ段（列）に紫色のマスが１つしかない箇所を探して「７」を確定する
・「７」が入る可能性のなくなったマスを消す
の繰り返しで「７」を確定させていく。
★ちなみにこちらは「７」が確定した瞬間にその段（列）と重複する紫色のマスを消しています。
もちろん（？）こちらもこの作業だけでは全ての「７」が確定できない場合もあるので、とりあえずは確定できるところまで最小数字と最大数字を入れる。
③同じ不等号が続く箇所を探す
言葉だけだといまいち分かりにくいテクニックだが、この例題でいうと下図の「１」＜「ａ」＜「ｂ」＜「ｃ」＜「ｄ」＜「ｅ」のマスのような箇所である。こういう箇所は入る数字の組み合わせが限定できるので数字を確定させやすい。
今回の場合、「連続するマスが６つ」で「（連続する部分の）最小数字が１」なので、ａ～ｅに入る数字の組み合わせは「２３４５６」「２３４５７」「２３４６７」「２３５６７」「２４５６７」「３４５６７」の６通りに限定できる。
そして今回の場合既に全ての段（列）に「７」が確定している（ａ～ｅの中に「７」を使う事は出来ない）ので、可能性として残るのは「２３４５６」の組み合わせしかない。よってａ～ｅの５マスに入る数字が順に「２」「３」「４」「５」「６」と確定する。
④数字の大小関係に注目する
ある程度数字が確定すると数字の大小関係から確定できるマスが出てくる。
・例えば左から２列目。１，２，３，６，７の５つの数字が確定しており、残る数字は「４」「５」。
残る２つのマス（紫色のマス）には運のいい事に（？）不等号による直接の大小関係が成立しているので、上のマスが「４」、下のマスが「５」に確定する。
・隣の列（左から３列目、緑色のマス）も同様に３つのマスに直接の大小関係が成立しているので、上から「６」「３」「２」と確定する。
・上から２段目中央の（赤色の）マスは左右の数字と不等号から「１より大きく４より小さい数字」が入る事になる。
その条件に合致する数字は「２」か「３」の２つのみ（小数や分数は普通のナンプレでは使えない）で、そのうち「３」は既に同じ段に確定していて入れることが出来ないのでこのマスには「２」が確定する。
⑤消去法で数字を確定する
今までのテクニックより高度というより複雑なテクニックだが、これを知らないと解けない不等号ナンプレは（主に初期ヒントの少ない問題に）多い。
下図の「Ａ」のマスについて考える。同じ段には１，２，４，７が確定しているので、入る可能性のある数字は「３」「５」「６」のどれかである。
・「６」を入れようとするとその左のマスには不等号の関係から６より大きい数字が入る事になる。
このナンプレで６より大きい数字となると「７」しかないが、その「７」はそのマスのすぐ下のマスに確定しているので「Ａ」の左のマスに入れるべき数字がなくなってしまう（「６＜○＜７」を満たせる数字が存在しない）。つまり「Ａ」に「６」を入れることは出来ない、という事になる。
・「５」を入れようとするとその左のマスは「６」になる。同時に不等号の関係から「Ａ（５）」の下のマスも「６」になる。
…一見上手く行きそうだが、「Ａ（５）」の上のマスは不等号の関係から「５＜○＜７」を満たす数字、この場合「６」が入るべきなのだが、その「６」は先ほど「５」の下のマスに使ってしまった（同じ列に重複してしまう）ため入れることが出来ない。
更に言うとその（一番下の段の）「６」の右のマスも不等号の関係から入れる数字がなくなってしまう（「７」は同じ段・列に既に使われている）。故に遡って「Ａ」に「５」を入れることは出来ない、という事になる。
・その結果、「Ａ」に入る可能性のある数字は「３」に絞られるので「Ａ」は「３」に確定する。
同様の理屈で「Ｂ」を考えると、
・入る可能性のある数字は「５」か「６」。
・「６」を入れようとするとその上のマスには「６＜○＜７」を満たす数字が必要になるが、そういう数字は存在しない。つまり「Ｂ」に「６」を入れることは出来ない。
・よって「Ｂ」は「５」に確定する。同時に同じ段（下から２段目）の残ったマスは「６」に確定、「Ｂ」の上のマスも「５＜○＜７」を満たす数字、つまり「６」に確定する。
最初はノーヒントでもこのようにあっという間に（？）半分以上（４９マス中２９マス）が確定するのである。
ここから先は「読者（解答者）のお楽しみ」という事で割愛するが、残りのマスも同様に上記③④⑤のテクニックを使う事で解く事ができる。
…さて、ここまで読んでいただいて不等号ナンプレの魅力（？）は伝わっただろうか。
…え？ 全然伝わらん？ …尚更嫌いになった？
困りましたねぇ… 面倒なテクニック（冒頭にあった「浜田ロジック」など）を要する難問スタンダードナンプレを解くよりはずっと楽しいと思うのだけどなぁ…
もしかして画像がチカチカするのがいけなかったのかしら…（笑）
この調子だとただでさえ少ないこのブログの読者がますます少なくなりそうである（笑）。
既に脳内には次回のプランが出来ている（故にタイトルに「～・１」と打っている）のだが…
